[SORT] Selection Sort (선택 정렬)

Goal

• 정렬 알고리즘 중 Selection Sort 에 대해 알기
• Selection Sort의 장· 단점
• 시간 복잡도 이해하기
• 자바로 구현할 줄 알기

Selection Sort (선택 정렬) 알고리즘

데이터 중에서 가장 작은(가장 큰) 데이터를 선택해 현재의 데이터와 위치 교환하는 방식

아래 예시를 통해 이해해 보자

PASS 1 - 주어진 배열 중에서 최솟값을 찾는다.

PASS 2 - 현재 위치 값과 Min 값을 SWAP 한다.

가장 작은 데이터 (Min)값이 배열의 맨 앞자리로 이동했다.

그렇다면 배열의 첫번째 데이터는 최솟값 고정이므로 현재 위치(ptr) 를 다음 index로 이동시킨다.

PASS 3 현재 위치를 다음 index 로 이동시키고, 남은 데이터들 중에서 다시 Min 값을 찾는다.

PASS 2와 같은 방식으로 Min 값과 현재 위치(ptr)를 SWAP 한다.

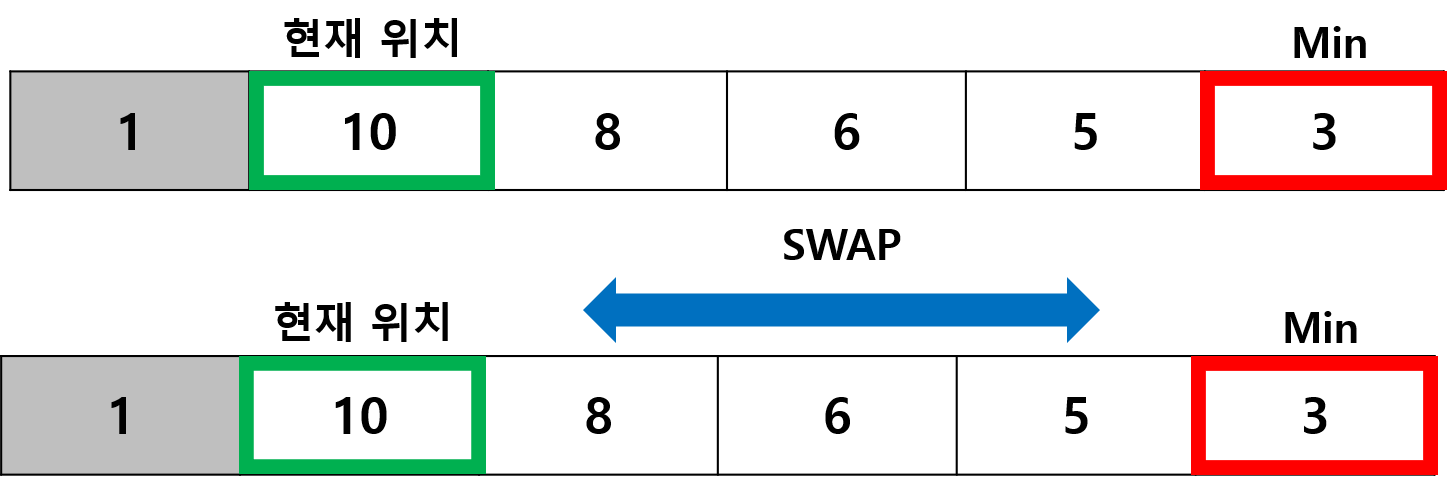
PASS 4 다음 방식을 계속해서 반복한다.

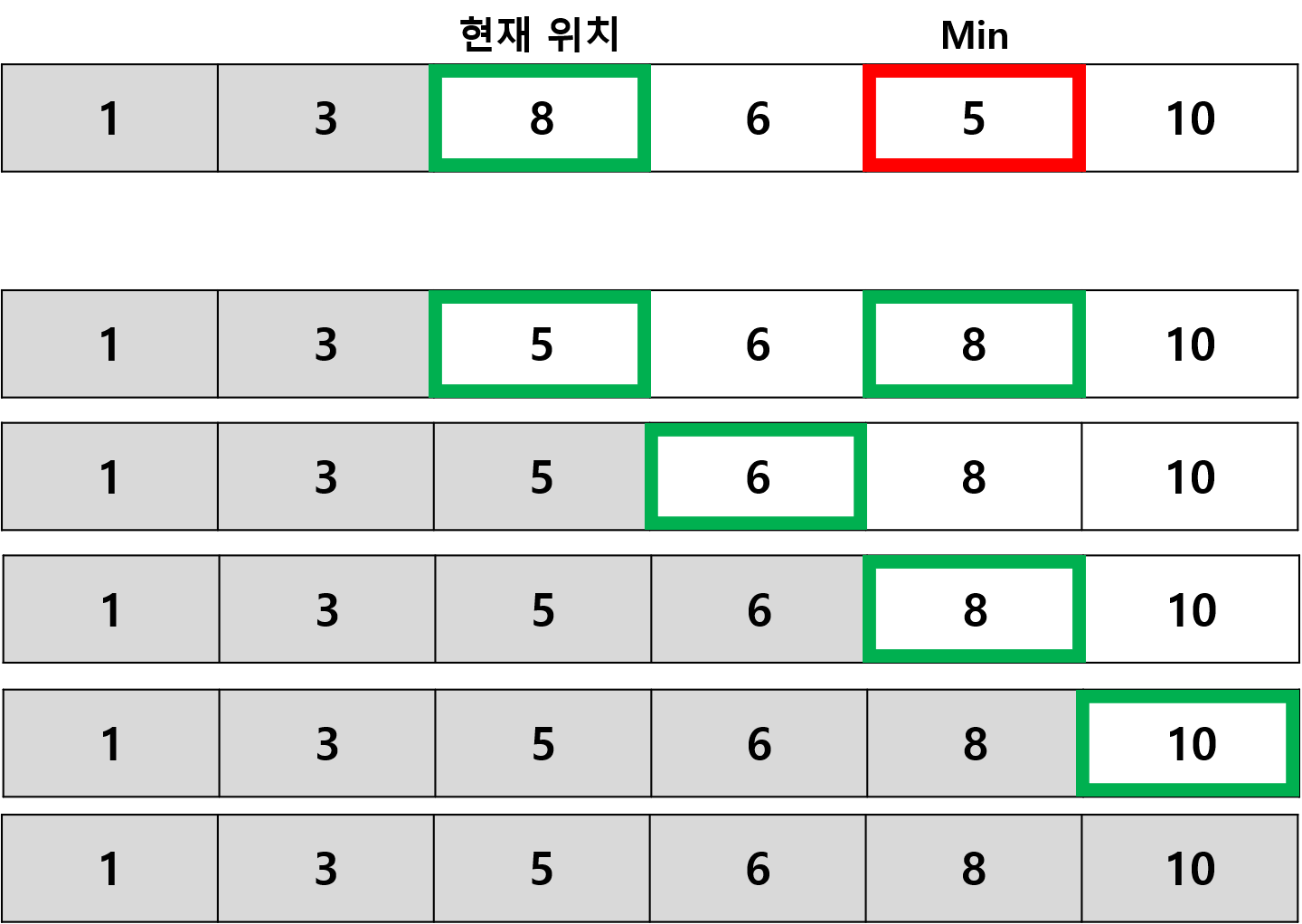
최솟값을 찾아서 Sort 하는 것으로 예시를 들어봤다.

이러한 방식으로 최댓값을 찾아서 현 위치(ptr)을 맨 뒤에 놓고, 거꾸로 가는 방식도 있다.

---

Selection Sort (선택 정렬) 의 장 · 단점

• 장점 :
  • 구현이 단순하다.
  • Bubble Sort보다 이동이 적어 비교적 빠르다.
• 단점 :
  • 데이터 크기가 커질수록 효율이 떨어진다.
  • 시간복잡도가 항상 O(n^2) 고정으로 오래걸린다.

---

Selection Sort (선택 정렬) 의 시간복잡도

Selection Sort : O(n^2)

위의 예시를 통해 이해해 보자.

**데이터 개수가 6개일 때 **

첫 For 문에서 arr[0]을 제외한 나머지 5개에서 Min 을 찾는다. -> 비교 횟수 5개 (n-1)

다음으로는 arr[1]을 제외한 나머지 4개에서 Min 을 찾는다. -> 비교 횟수 4개 (n-2)

데이터 개수 n 개로 다시 적용해보자.

i == 0 : arr[1] ~ arr[n-1] - 비교 횟수 n-1 번

i == 1 : arr[2] ~ arr[n-1] - 비교 횟수 n-2 번

i == 2 : arr[3] ~ arr[n-2] - 비교 횟수 n-3 번

​ .

​ .

i == n-1 : arr[n-1] - 비교 횟수 1번

전체 합 : (n-1) + (n-2) + (n-3) + ….. + 2 + 1 => n(n-1) / 2*

결과 : 데이터가 n 개일 때 걸리는 시간 복잡도는 O(n^2) 입니다.

---

Selection Sort (선택 정렬) JAVA 구현

public class SelectionSort {
	public static void main(String[] args) throws IOException {
		BufferedReader br = new BufferedReader(new InputStreamReader(System.in));
		StringBuilder sb = new StringBuilder();

		int n = Integer.valueOf(br.readLine());
		int[] arr = new int[n];
		for (int i = 0; i < n; i++) {
			arr[i] = Integer.valueOf(br.readLine());
		}

		int min = arr[0];
		for (int i = 0; i < n; i++) {
			int index = i;
			for (int j = i; j < n - 1; j++) {
				if (arr[j] > arr[j + 1]) {
					min = arr[j + 1];
					index = j + 1;
				}
			}
			sb.append("SWAP " + arr[i] + "  <-->  " + arr[index] + "\n");
			int temp = arr[i];
			arr[i] = min;
			arr[index] = temp;
		}

		for (int i = 0; i < n; i++) {
			sb.append(arr[i] + " ");
		}
		System.out.println(sb);
	}

}

윗 예시를 코드를 통해 똑같이 적용.

n = 6, array = [5, 10, 8, 6, 1, 3]